On this page

Computing the Lagrangian Descriptors of Dynamical Systems

GitHub repo

The library pylds can downloaded from https://github.com/broncio123/lds

NOTE This is part of an ongoing software development project by the CHAMPS group.

No guarantee the code is bug-free. Contact the developers or raise an issue in the repo for any problems you encounter.

Basic setup: IMPORTANT

BEFORE running this Notebook we assume the following

  • This notebook runs with Python Version >= 3

  • conda si up-to-date. If not, in the terminal (Linux/Mac) or the Conda Prompt (Windows)

conda update --all

If you’re running this notebook and it works fine. That’s good news!

If you get error, please, try the proposed instructions in the next Subsection.

Package requirements

  • DO RUN the following lines, only if the current Notebook doesn’t execute properly.

  • DON’T RUN the following lines, if requirements.txt already satisfied or if Notebook runs fine.

If pip not installed within conda environment, execute the cell below

conda install pip==20.0.2

Install package dependencies

pip install -r requeriments.txt

Benchmark examples

import pylds
from pylds.base import compute_lagrangian_descriptor, perturb_field
from pylds.tools import draw_lagrangian_descriptor
from pylds.vector_fields import HamCenter1D, HamSaddle1D, Duffing1D, HamSN1D, Duffing1D_inverted, forcing, HenonHeiles_potential, HenonHeiles_vector_field, NFSaddle_potential, NFSaddle_vector_field

# Integration parameters
tau = 12

# LDp, p-value
p_value = 0.5

# Mesh parameters
x_min,x_max = [-1.6, 1.6]
y_min,y_max = [-1, 1]
Nx, Ny = [100, 100]

Some simple systems

Hamilton Centre

Energy

\begin{equation*} H(x, p_x) = \frac{\omega}{2} (p_x^2 + x^2), \quad \omega > 0 \end{equation*}

Vector field

\[\begin{split}\begin{align*} \dot{x} &= \frac{\partial H}{\partial p_x} = f_1(x, p_x) = \omega p_x \\ \dot{p}_x &= -\frac{\partial H}{\partial x} = f_2(x, p_x) = -\omega x \end{align*}\end{split}\]
# Integration parameters
tau = 12

# LDp, p-value
p_value = 0.5

# Mesh parameters
x_min,x_max = [-1.6, 1.6]
y_min,y_max = [-1, 1]
Nx, Ny = [100, 100]

grid_parameters = [(x_min, x_max, Nx), (y_min, y_max, Ny)]
vector_field = HamCenter1D

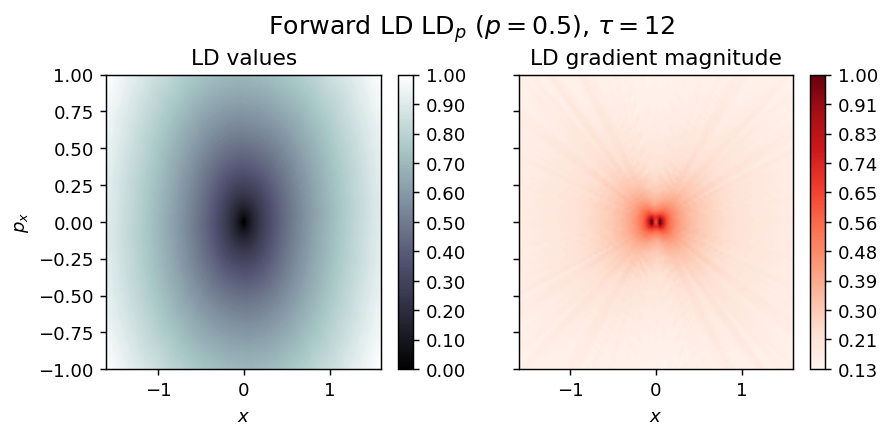
LD_forward = compute_lagrangian_descriptor(grid_parameters, vector_field, tau, p_value)
draw_lagrangian_descriptor(LD_forward, 'forward', grid_parameters, tau, p_value)

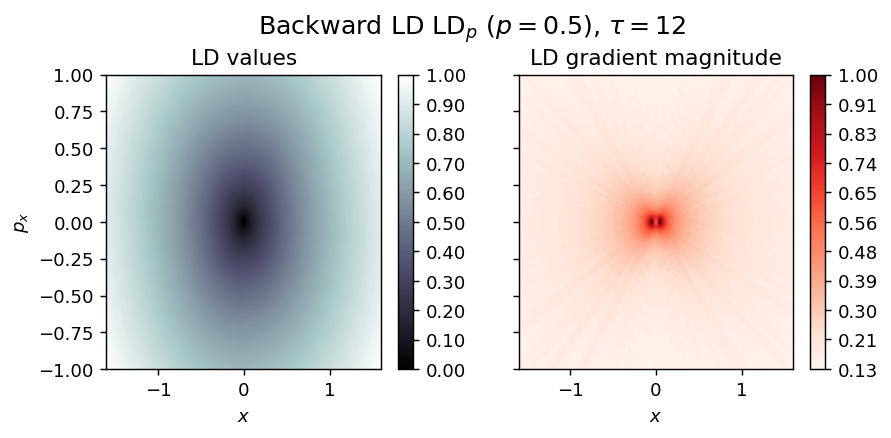
LD_backward = compute_lagrangian_descriptor(grid_parameters, vector_field, -tau, p_value)
draw_lagrangian_descriptor(LD_backward, 'backward', grid_parameters, tau, p_value)

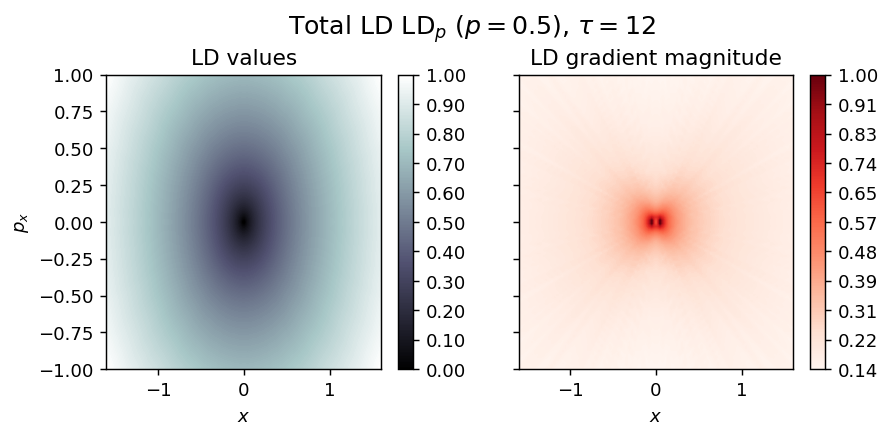
LD_total = LD_forward + LD_backward
draw_lagrangian_descriptor(LD_total, 'total', grid_parameters, tau, p_value)
../_images/examples_12_0.png ../_images/examples_12_1.png ../_images/examples_12_2.png

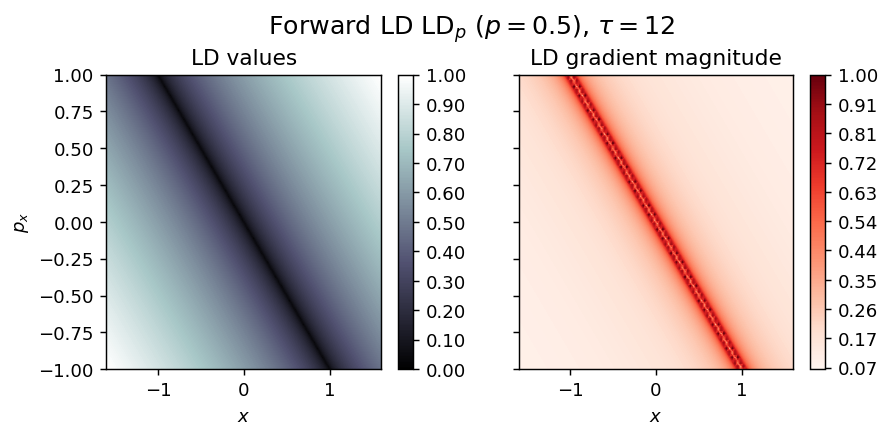
Hamilton Saddle

Energy

\begin{equation*} H(x, p_x) = \frac{\lambda}{2}( p_x^2 - x^2 ), \quad \lambda > 0 \end{equation*}

Vector field

\[\begin{split}\begin{align*} \dot{x} &= \frac{\partial H}{\partial p_x} = f_1(x, p_x) = -\lambda p_x \\ \dot{p}_x &= -\frac{\partial H}{\partial x} = f_2(x, p_x) = \lambda x \end{align*}\end{split}\]
# Integration parameters
tau = 12

# LDp, p-value
p_value = 0.5

# Mesh parameters
x_min,x_max = [-1.6, 1.6]
y_min,y_max = [-1, 1]
Nx, Ny = [100, 100]

grid_parameters = [(x_min, x_max, Nx), (y_min, y_max, Ny)]
vector_field = HamSaddle1D

LD_forward = compute_lagrangian_descriptor(grid_parameters, vector_field, tau, p_value)
draw_lagrangian_descriptor(LD_forward, 'forward', grid_parameters, tau, p_value)

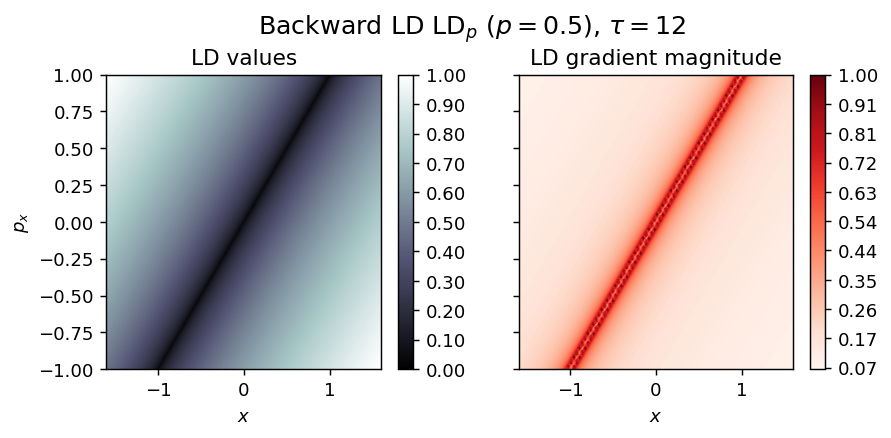
LD_backward = compute_lagrangian_descriptor(grid_parameters, vector_field, -tau, p_value)
draw_lagrangian_descriptor(LD_backward, 'backward', grid_parameters, tau, p_value)

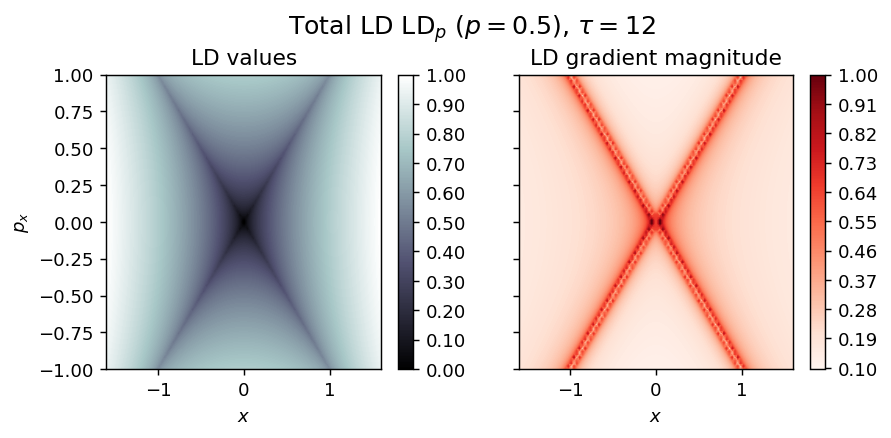
LD_total = LD_forward + LD_backward
draw_lagrangian_descriptor(LD_total, 'total', grid_parameters, tau, p_value)
../_images/examples_17_0.png ../_images/examples_17_1.png ../_images/examples_17_2.png

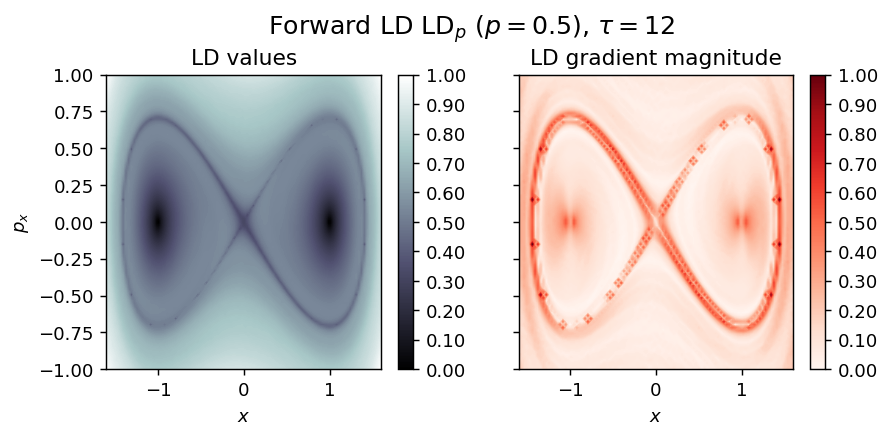
Duffing oscillator

Energy

\begin{equation*} H(x, p_x) = \frac{1}{2} (p_x^2 - x^2 + \frac{1}{2} x^4) \end{equation*}

Vector field

\[\begin{split}\begin{align*} \dot{x} &= \frac{\partial H}{\partial p_x} = f_1(x, p_x) = p_x \\ \dot{p}_x &= -\frac{\partial H}{\partial x} = f_2(x, p_x) = x - x^3 \end{align*}\end{split}\]
# Integration parameters
tau = 12

# LDp, p-value
p_value = 0.5

# Mesh parameters
x_min,x_max = [-1.6, 1.6]
y_min,y_max = [-1, 1]
Nx, Ny = [100, 100]

grid_parameters = [(x_min, x_max, Nx), (y_min, y_max, Ny)]
vector_field = Duffing1D

LD_forward = compute_lagrangian_descriptor(grid_parameters, vector_field, tau, p_value)
draw_lagrangian_descriptor(LD_forward, 'forward', grid_parameters, tau, p_value)

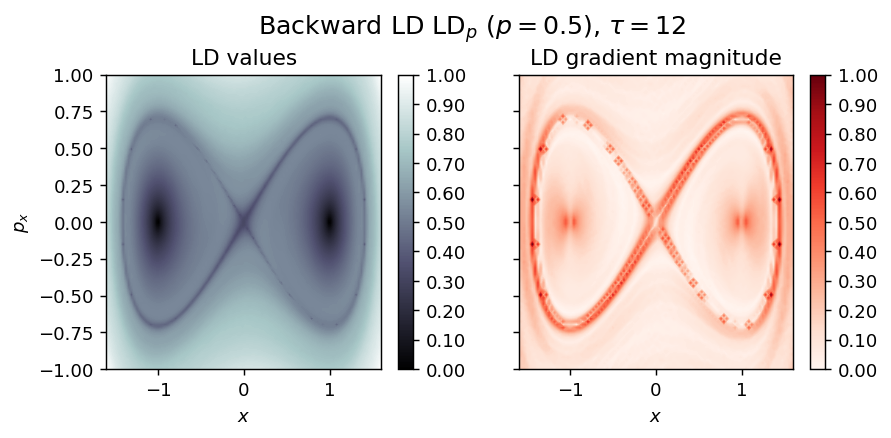
LD_backward = compute_lagrangian_descriptor(grid_parameters, vector_field, -tau, p_value)
draw_lagrangian_descriptor(LD_backward, 'backward', grid_parameters, tau, p_value)

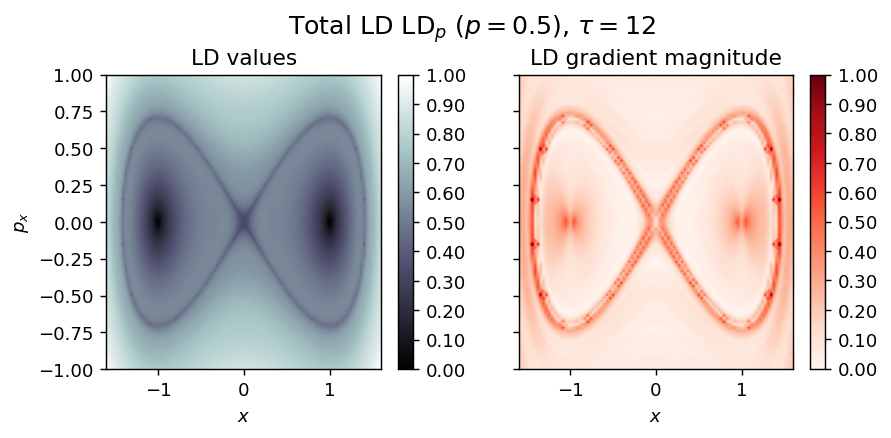
LD_total = LD_forward + LD_backward
draw_lagrangian_descriptor(LD_total, 'total', grid_parameters, tau, p_value)
../_images/examples_22_0.png ../_images/examples_22_1.png ../_images/examples_22_2.png

Example of a perturbed system

Harmonically perturbed Duffing oscillator

Energy

\begin{equation*} H(x, p_x, t) = \frac{1}{2} (p_x^2 - x^2 + \frac{1}{2} x^4) \end{equation*}

Vector field whith time-dependent harmonic forcing

\[\begin{split}\begin{align*} \dot{x} &= \frac{\partial H}{\partial p_x} = f_1(x, p_x) = p_x \\ \dot{p}_x &= -\frac{\partial H}{\partial x} + + \eta(t) = f_2(x, p_x) = x - x^3 + \eta(t) \end{align*}\end{split}\]

where

\begin{align*} \eta(t) = A \cdot sin(\omega t) \end{align*}

with \(A\) and \(\omega\) the amplitude and the frequency of the perturbation.

# Integration parameters
tau = 12

# LDp, p-value
p_value = 0.5

# Mesh parameters
x_min,x_max = [-1.6, 1.6]
y_min,y_max = [-1, 1]
Nx, Ny = [100, 100]

grid_parameters = [(x_min, x_max, Nx), (y_min, y_max, Ny)]
vector_field_original = Duffing1D
vector_field = perturb_field(vector_field_original, forcing)

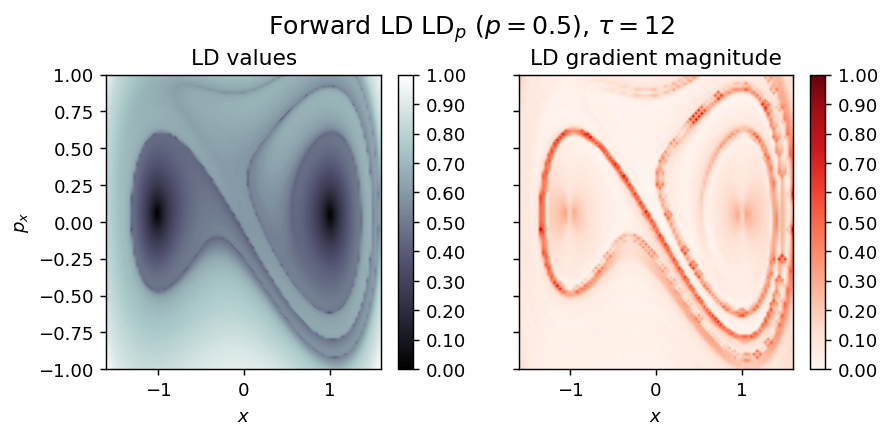
LD_forward = compute_lagrangian_descriptor(grid_parameters, vector_field, tau, p_value)
draw_lagrangian_descriptor(LD_forward, 'forward', grid_parameters, tau, p_value)

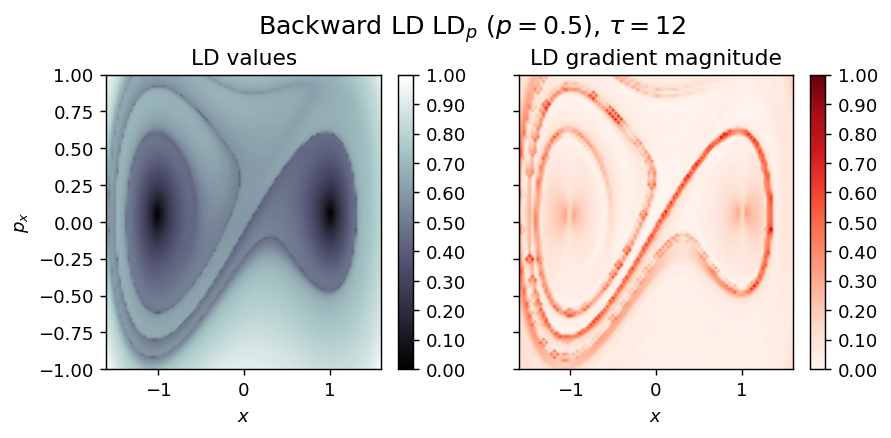
LD_backward = compute_lagrangian_descriptor(grid_parameters, vector_field, -tau, p_value)
draw_lagrangian_descriptor(LD_backward, 'backward', grid_parameters, tau, p_value)

LD_total = LD_forward + LD_backward
draw_lagrangian_descriptor(LD_total, 'total', grid_parameters, tau, p_value)
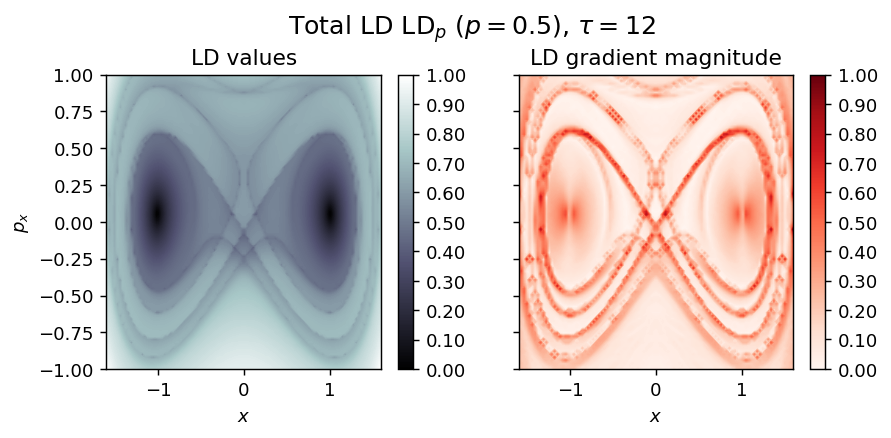
../_images/examples_28_0.png ../_images/examples_28_1.png ../_images/examples_28_2.png

Example of systems that blow up in finite time

Hamilton Saddle-Node

Energy

\begin{equation*} H(x, p_x) = \frac{1}{2} (p_x^2 + x^2 + \frac{2}{3} x^3) \end{equation*}

Vector field

\[\begin{split}\begin{align*} \dot{x} &= \frac{\partial H}{\partial p_x} = f_1(x, p_x) = p_x \\ \dot{p}_x &= -\frac{\partial H}{\partial x} = f_2(x, p_x) = -x - x^2 \end{align*}\end{split}\]
# Integration parameters
t0 = 0
tau = 8
dt = 0.1

# Lp-norm, p-value
p_norm = 1/2

# Mesh parameters
x_min,x_max = [-1.5, 1]
y_min,y_max = [-1, 1]

# Box boundaries for Variable Time Integration
box_x_min, box_x_max = [-6, 6]

grid_parameters = [(x_min, x_max, Nx), (y_min, y_max, Ny)]
vector_field = HamSN1D
box_boundaries = [(box_x_min, box_x_max)]

LD_forward = compute_lagrangian_descriptor(grid_parameters, vector_field, tau, p_value, box_boundaries)
draw_lagrangian_descriptor(LD_forward, 'forward', grid_parameters, tau, p_value)

LD_backward = compute_lagrangian_descriptor(grid_parameters, vector_field, -tau, p_value, box_boundaries)
draw_lagrangian_descriptor(LD_backward, 'backward', grid_parameters, tau, p_value)

LD_total = LD_forward + LD_backward
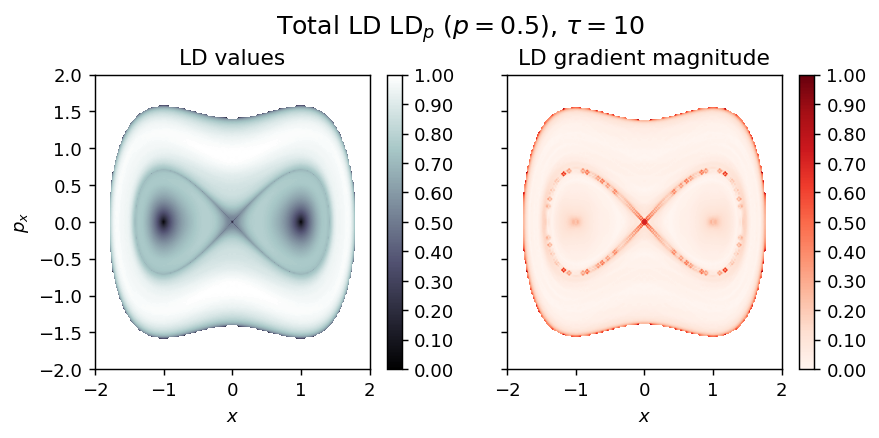
draw_lagrangian_descriptor(LD_total, 'total', grid_parameters, tau, p_value, box_boundaries)
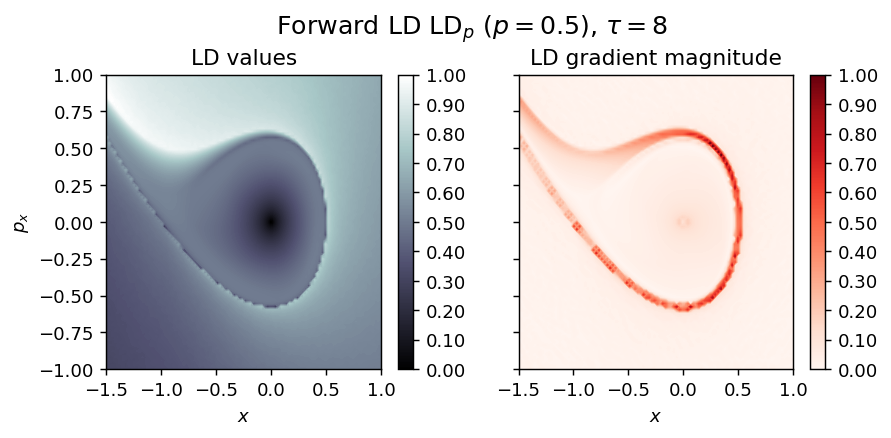
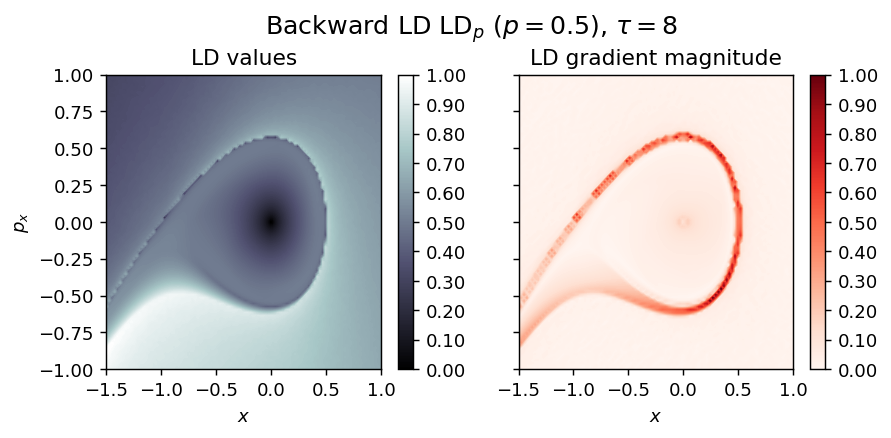
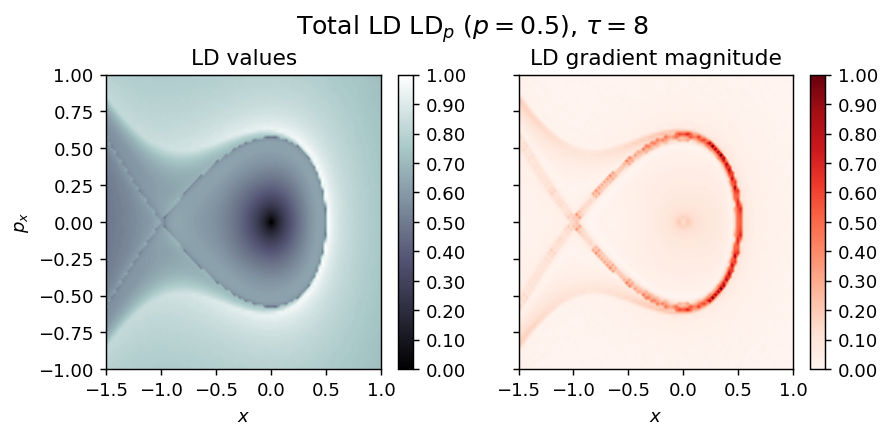
../_images/examples_34_0.png ../_images/examples_34_1.png ../_images/examples_34_2.png

Inverted Duffing oscillator

Energy

\begin{equation*} H(x, p_x) = \frac{1}{2} (p_x^2 + x^2 - \frac{1}{2} x^4) \end{equation*}

Vector field

\[\begin{split}\begin{align*} \dot{x} &= \frac{\partial H}{\partial p_x} = f_1(x, p_x) = p_x \\ \dot{p}_x &= -\frac{\partial H}{\partial x} = f_2(x, p_x) = -x + x^3 \end{align*}\end{split}\]
# Integration parameters
t0 = 0
tau = 10
dt = 0.1

# Lp-norm, p-value
p_norm = 1/2

# Mesh parameters
x_min,x_max = [-1.5, 1.5]
y_min,y_max = [-1, 1]

# Box boundaries for Variable Time Integration
box_x_min, box_x_max = [-6, 6]

grid_parameters = [(x_min, x_max, Nx), (y_min, y_max, Ny)]
vector_field = Duffing1D_inverted
box_boundaries = [(box_x_min, box_x_max)]

LD_forward = compute_lagrangian_descriptor(grid_parameters, vector_field, tau, p_value, box_boundaries)
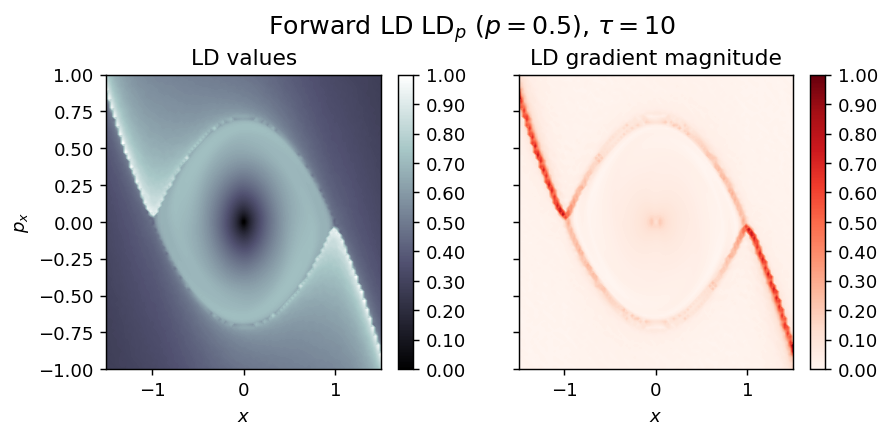
draw_lagrangian_descriptor(LD_forward, 'forward', grid_parameters, tau, p_value)

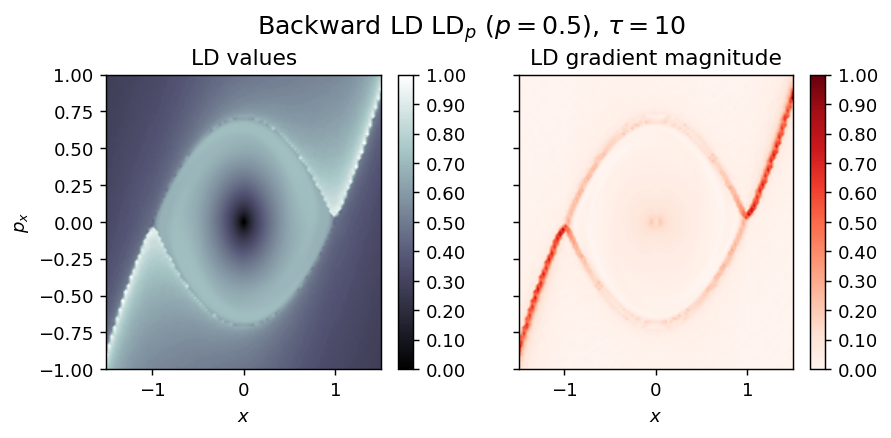
LD_backward = compute_lagrangian_descriptor(grid_parameters, vector_field, -tau, p_value, box_boundaries)
draw_lagrangian_descriptor(LD_backward, 'backward', grid_parameters, tau, p_value)

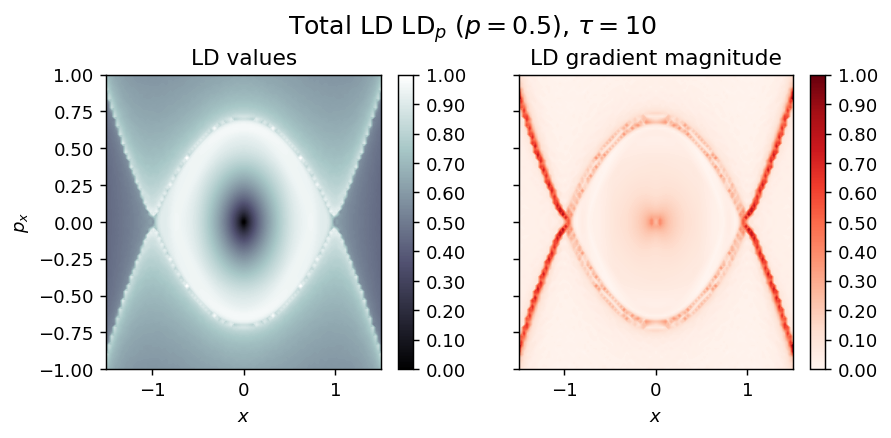
LD_total = LD_forward + LD_backward
draw_lagrangian_descriptor(LD_total, 'total', grid_parameters, tau, p_value, box_boundaries)
../_images/examples_39_0.png ../_images/examples_39_1.png ../_images/examples_39_2.png

High-dimensional Hamiltonian systems

Energy

\begin{equation*} H(x, p_x) = K + V = \frac{1}{2} (p_x^2 + p_y^2) + x^2 y - \frac{1}{3} y^3 \end{equation*}

Vector field

\[\begin{split}\begin{align*} \dot{x} &= \frac{\partial H}{\partial p_x} = p_x \\ \dot{y} &= \frac{\partial H}{\partial p_y} = p_y \\ \dot{p}_x &= -\frac{\partial H}{\partial x} = -x - 2 x y \\ \dot{p}_y &= -\frac{\partial H}{\partial y} = -x^2 -y + y^2 \\ \end{align*}\end{split}\]

Henon-Heiles

# Integration parameters
t0 = 0
tau = 50

# Lp-norm, p-value
p_value = 1/2

# Mesh visualisation slice parameters
H0 = 1/5 # Energy

ax1_min,ax1_max = [-0.6, 1.2]
ax2_min,ax2_max = [-0.65, 0.65]
N1, N2 = [160, 160]

# Box escape condition
box_boundaries = [[-5, 5], [-5, 5]]

# Miscellaneous grid parameters
dims_fixed = [1,0,0,0] # Variable ordering (x1 x2 y1 y2)
dims_fixed_values = [0] # This can also be an array of values
dims_slice = [0,1,0,1] # Visualisation slice
momentum_sign = 1 # Direction of momentum that defines the slice - (1) positive / (-1) negative

potential_energy = HenonHeiles_potential
vector_field = HenonHeiles_vector_field

slice_parameters = [[ax1_min, ax1_max, N1],[ax2_min, ax2_max, N2]]

grid_parameters = {
        'slice_parameters' : slice_parameters,
        'dims_slice' : dims_slice,
        'dims_fixed' : [dims_fixed, dims_fixed_values],
        'momentum_sign' : momentum_sign,
        'potential_energy': potential_energy,
        'energy_level': H0
    }

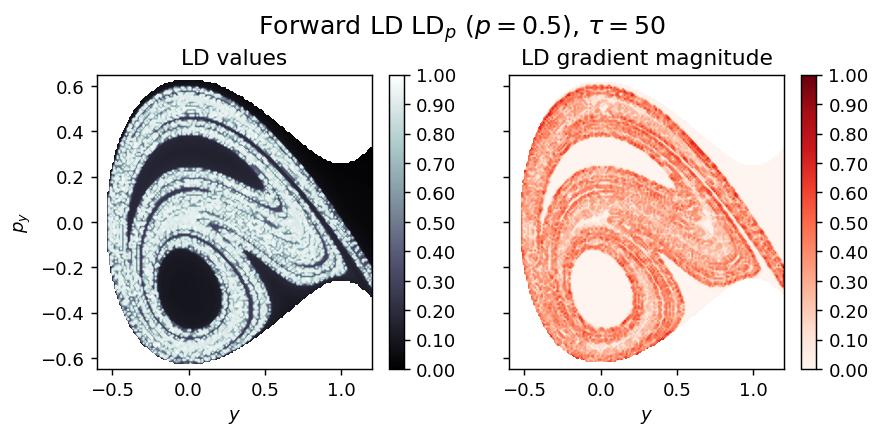
LD_forward = compute_lagrangian_descriptor(grid_parameters, vector_field, tau, p_value, box_boundaries)
draw_lagrangian_descriptor(LD_forward, 'forward', grid_parameters, tau, p_value)

LD_backward = compute_lagrangian_descriptor(grid_parameters, vector_field, -tau, p_value, box_boundaries)
draw_lagrangian_descriptor(LD_backward, 'backward', grid_parameters, tau, p_value)

LD_total = LD_forward + LD_backward
draw_lagrangian_descriptor(LD_total, 'total', grid_parameters, tau, p_value)

/Users/ba13026/research/lagrangian_descriptors/book/content/pylds/base.py:22: RuntimeWarning: invalid value encountered in sqrt
  np.sqrt(2*(H0 - V) - (phase_space_momenta**2).sum(axis=1))
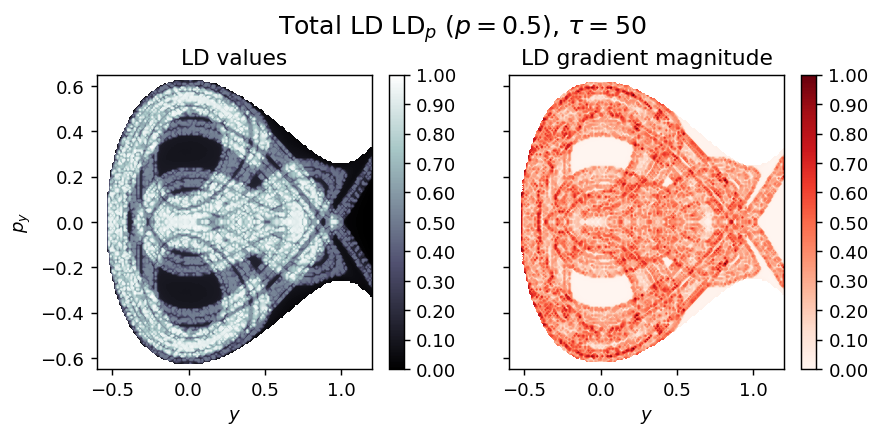
../_images/examples_45_1.png ../_images/examples_45_2.png ../_images/examples_45_3.png

Index-1 Normal Form Saddle

Energy

\begin{equation*} H(x, p_x) = K + V = \frac{1}{2} (p_x^2 + p_y^2) + \frac{1}{2}(y^2 - x^2) \end{equation*}

Vector field

\[\begin{split}\begin{align*} \dot{x} &= \frac{\partial H}{\partial p_x} = p_x \\ \dot{y} &= \frac{\partial H}{\partial p_y} = p_y \\ \dot{p}_x &= -\frac{\partial H}{\partial x} = x \\ \dot{p}_y &= -\frac{\partial H}{\partial y} = -y \\ \end{align*}\end{split}\]
# Integration parameters
t0 = 0
tau = 10

# Lp-norm, p-value
p_value = 1/2

# Mesh visualisation slice parameters
H0 = 1 # Energy
ax1_min,ax1_max = [-2, 2]
ax2_min,ax2_max = [-2, 2]
N1, N2 = [100, 100]

# Box escape condition
box_boundaries = False

# Miscellaneous grid parameters
dims_fixed = [0,1,0,0] # Variable ordering (x1 x2 y1 y2)
dims_fixed_values = [0] # This can also be an array of values
dims_slice = [1,0,1,0] # Visualisation slice
momentum_sign = -1 # Direction of momentum that defines the slice - (1) positive / (-1) negative

potential_energy = NFSaddle_potential
vector_field = NFSaddle_vector_field

slice_parameters = [[ax1_min, ax1_max, N1],[ax2_min, ax2_max, N2]]

grid_parameters = {
        'slice_parameters' : slice_parameters,
        'dims_slice' : dims_slice,
        'dims_fixed' : [dims_fixed, dims_fixed_values],
        'momentum_sign' : momentum_sign,
        'potential_energy': potential_energy,
        'energy_level': H0
    }

LD_forward = compute_lagrangian_descriptor(grid_parameters, vector_field, tau, p_value)
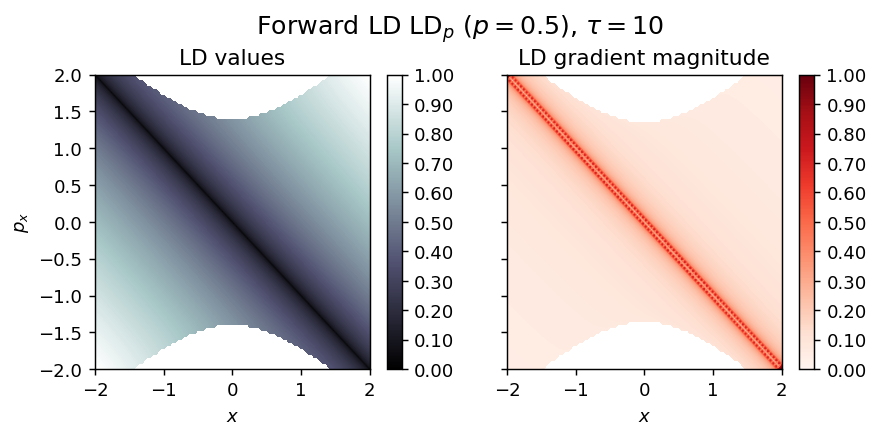
draw_lagrangian_descriptor(LD_forward, 'forward', grid_parameters, tau, p_value)

LD_backward = compute_lagrangian_descriptor(grid_parameters, vector_field, -tau, p_value)
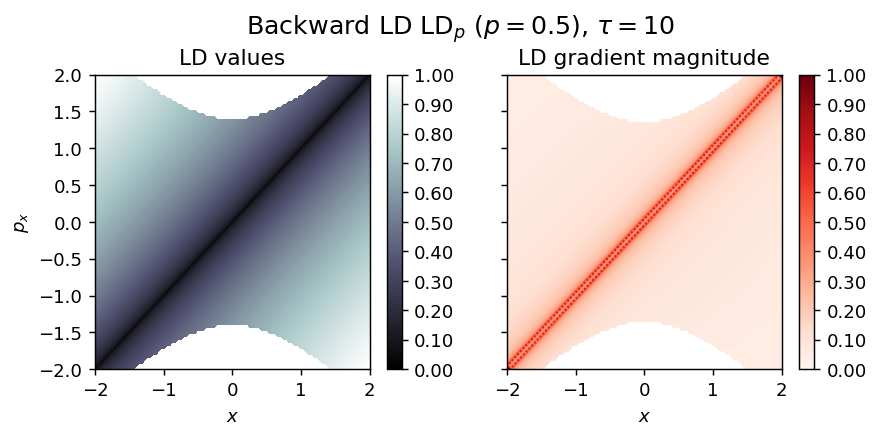
draw_lagrangian_descriptor(LD_backward, 'backward', grid_parameters, tau, p_value)

LD_total = LD_forward + LD_backward
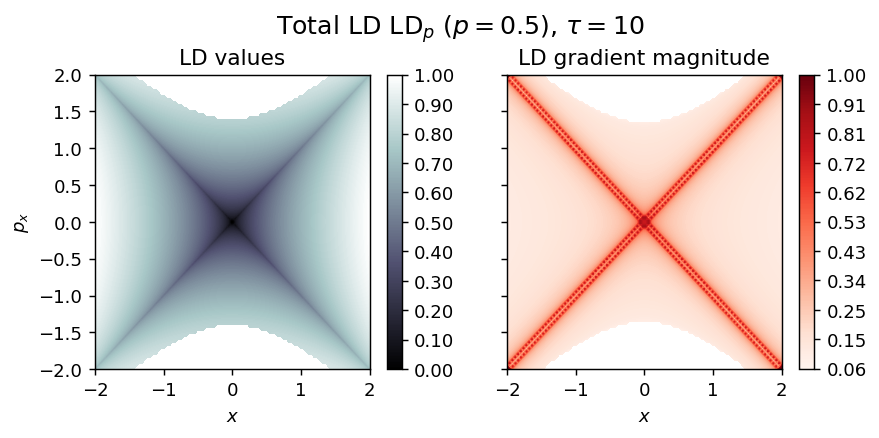
draw_lagrangian_descriptor(LD_total, 'total', grid_parameters, tau, p_value)
../_images/examples_50_0.png ../_images/examples_50_1.png ../_images/examples_50_2.png

HOW-TOs

Change parameters of built-in vector fields

  • EXAMPLE Changed default parameters for a vector field

FIRST Check vector field parameters using help

import pylds
help(pylds.vector_fields.HamCenter1D)

Help on function HamCenter1D in module pylds.vector_fields:

HamCenter1D(t, u, PARAMETERS=[1])
    Returns 1D Hamilton-Centre vector field at time t, for an array of points in phase space.
    Number of model parameters: 1 . PARAMETERS = [omega]
    Functional form: v = (omega*y, - omega*x), with u = (x, y)
    
    Parameters
    ----------
    t : float
        fixed time-point of vector field, for all points in phase space
        
    u : array_like, shape(n,)
        points in phase space to determine vector field at time t
    
    PARAMETERS : list of floats
        vector field parameters
    
    Returns
    -------
    v : array_like, shape(n,)
        vector field corresponding to points u, in phase space at time t

SECOND Define the input vector_field to compute LDs, just editing the value of PARAMETERS, here we set omega = 2.5

import pylds
vector_field = lambda t,u : pylds.vector_fields.HamCenter1D(t, u, PARAMETERS=[2.5])

  • EXAMPLE Changed default parameters for the forcing

Same as above. Define the input vector_field to compute LDs, just editing the value of PARAMETERS, here we set omega = 2.5

import pylds
vector_field = lambda t,u : pylds.vector_fields.HamCenter1D(t, u, PARAMETERS=[2.5])

Working with my own vector field: 1-DoF system

Setting up the code to draw the LDs of your own 1-DoF system requires only THREE simple steps

EXAMPLE

Suppose we have a 2D vector field of the form

\[\begin{split}\begin{align*} f_1(x, y) &= \alpha y \\ f_2(x, y) &= \beta \cdot cos(\gamma x^3) \end{align*}\end{split}\]

FIRST Define my_vector_field function

See how it’s done below

import numpy as np

def my_vector_field(t, u, PARAMETERS = [2, 0.5, 3]):
    """
    Returns a user-defined 1-DoF vector field at time t, for an array of points in phase-space.
    Number of model parameters: 1 . PARAMETERS = [alpha, beta, gamma]
    Functional form: v = (alpha*y, beta*x + gamma*x**4), with u = (x, y)
    
    Parameters
    ----------
    t : float
        fixed time-point of vector field, for all points in phase-space.
        
    u : array_like, shape(n,)
        points in phase-space to determine vector field at common time t.
    
    PARAMETERS : list of floats
        vector field parameters
    
    Returns
    -------
    v : array_like, shape(n,)
        vector field corresponding to points u, in phase-space at time t
    """
    x, y = u.T
    ##############################################
    #
    # CHANGE THIS STUFF BELOW ONLY
    #
    ##############################################
    # Hamiltonian Model Parameter
    alpha, beta, gamma = PARAMETERS
    v = np.array([ alpha * y, beta * np.cos(gamma * x**3)]).T
    ##############################################
    #
    # CHANGE THIS STUFF ABOVE ONLY
    #
    ##############################################    
    return v

Then, the input vector_field for computation of LDs will be

vector_field = my_vector_field

SECOND Set your general input parameters

import pylds

# Integration parameters
t0 = 0 # Starting time for integration
tau = 8 # Length integration
dt = 0.1 # Timestep

# Lp-norm, p-value
p_value = 1/2

# Mesh parameters
x_min,x_max = [-1.6, 1.6]
y_min,y_max = [-1, 1]
Nx, Ny = [160, 160]

grid_parameters = [(x_min, x_max, Nx), (y_min, y_max, Ny)] # Grid to sample Initial Conditions

THIRD Compute and Visualise your desired Lagrangian Descriptors

LD_forward = pylds.base.compute_lagrangian_descriptor(grid_parameters, vector_field, tau, p_value)
pylds.tools.draw_lagrangian_descriptor(LD_forward, 'forward', grid_parameters, tau, p_value, colormap_name='rainbow')
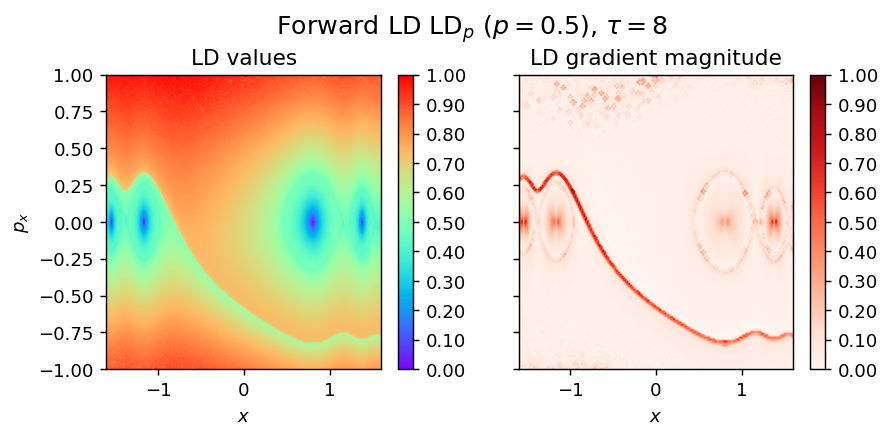
../_images/examples_73_0.png

Note The only difference for LD_backward is the integration time - tau

LD_backward = pylds.base.compute_lagrangian_descriptor(grid_parameters, vector_field, -tau, p_value)
pylds.tools.draw_lagrangian_descriptor(LD_backward, 'backward', grid_parameters, -tau, p_value, colormap_name='rainbow')
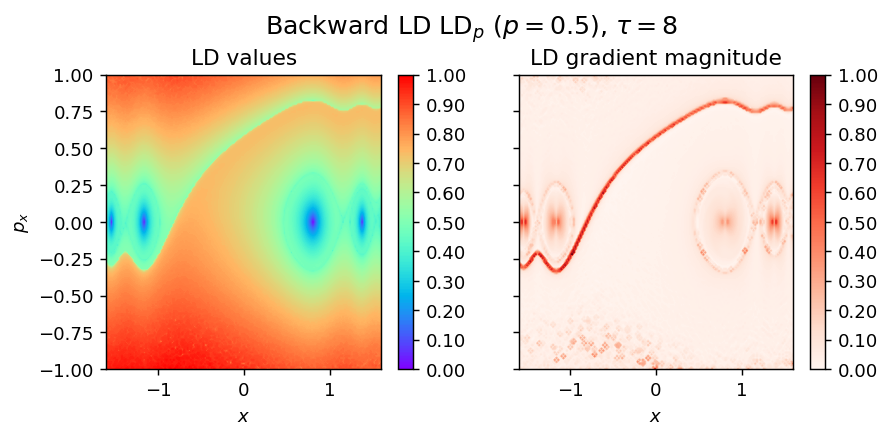
../_images/examples_75_0.png 
LD_total = LD_forward + LD_backward
pylds.tools.draw_lagrangian_descriptor(LD_total, 'total', grid_parameters, tau, p_value, colormap_name='rainbow')
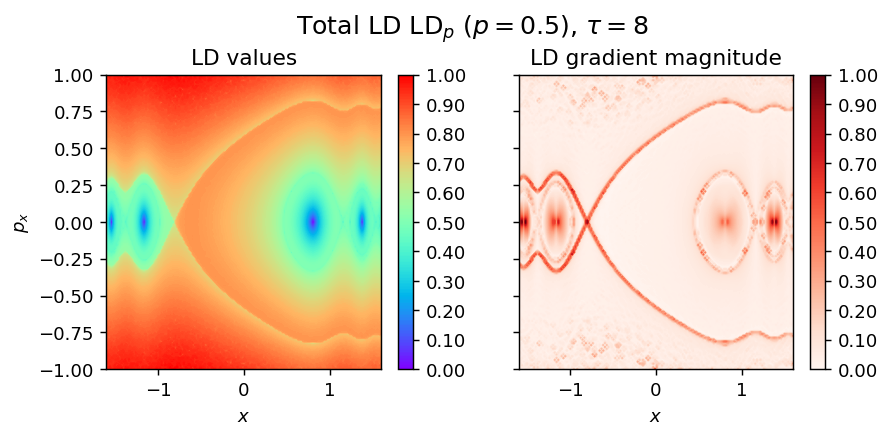
../_images/examples_76_0.png

Working with my own vector field: 2-DoF system

Setting up the code to draw the LDs of your own 2-DoF system requires only FOUR simple steps

EXAMPLE Here we chose a Hamiltonian system with a Double well potential

Energy

\begin{equation*} H(x, p_x) = K + V = \frac{1}{2} (p_x^2 + p_y^2) + \frac{1}{2}(y^2 - x^2 + \frac{1}{2} x^4) \end{equation*}

Vector field

\[\begin{split}\begin{align*} \dot{x} &= \frac{\partial H}{\partial p_x} = p_x \\ \dot{y} &= \frac{\partial H}{\partial p_y} = p_y \\ \dot{p}_x &= -\frac{\partial H}{\partial x} = x - x^3 \\ \dot{p}_y &= -\frac{\partial H}{\partial y} = -y \\ \end{align*}\end{split}\]

FIRST Define my_vector_field function

import numpy as np

def my_vector_field(t, u, PARAMETERS = [None]):
    """
    Returns 2-DoF vector field (Double Well system), for an array of points in phase space.
    Number of model parameters: 0 . PARAMETERS = [None]
    Functional form: v = (p_x, p_y, x - x**3, -y), with u = (x, y, p_x, p_y)
    
    Parameters
    ----------  
    t : float
        fixed time-point of vector field, for all points in phase space.
        
    u : array_like, shape(n,)
        Points in phase space.
        
    PARAMETERS : list of floats
        Vector field parameters.
    
    Returns
    -------
    v : array_like, shape(n,)
        Vector field corresponding to points u, in phase space at time t.
    """
    N_dims = u.shape[-1]
    points_positions = u.T[:int(N_dims/2)]
    points_momenta = u.T[int(N_dims/2):]
    x, y = points_positions
    p_x, p_y = points_momenta 
    
    # Hamiltonian Model Parameter
    
    # Vector field defintion
    v_x   =  p_x
    v_y   =  p_y
    v_p_x =  x - x**3
    v_p_y = -y
    v = np.array([v_x, v_y, v_p_x, v_p_y]).T
    return v

SECOND Define my_potential energy function

def my_potential(positions, PARAMETERS = None):
    x, y = positions.T
    # Function parameters
    # None
    # Potential energy function
    V = (1/4)*x**4 - (1/2)*x**2 + (1/2)*y**2
    return V

THIRD Set your general input parameters

# Integration parameters
t0 = 0
tau = 10

# Lp-norm, p-value
p_value = 1/2

# Mesh visualisation slice parameters
H0 = 1 # Energy level

ax1_min,ax1_max = [-2, 2]
ax2_min,ax2_max = [-2, 2]
N1, N2 = [200, 200]

# Box escape condition
box_boundaries = False

# Miscellaneous grid parameters
dims_fixed = [0,1,0,0] # Variable ordering (x y p_x p_y)
dims_fixed_values = [0] # This can also be an array of values
dims_slice = [1,0,1,0] # Visualisation slice
momentum_sign = 1 # Direction of momentum that defines the slice - (1) positive / (-1) negative

potential_energy = my_potential
vector_field = my_vector_field

slice_parameters = [[ax1_min, ax1_max, N1],[ax2_min, ax2_max, N2]]

grid_parameters = {
        'slice_parameters' : slice_parameters,
        'dims_slice' : dims_slice,
        'dims_fixed' : [dims_fixed, dims_fixed_values],
        'momentum_sign' : momentum_sign,
        'potential_energy': potential_energy,
        'energy_level': H0
    }

FOURTH Compute and Visualise your desired Lagrangian Descriptors

LD_forward = compute_lagrangian_descriptor(grid_parameters, vector_field, tau, p_value)
draw_lagrangian_descriptor(LD_forward, 'forward', grid_parameters, tau, p_value)
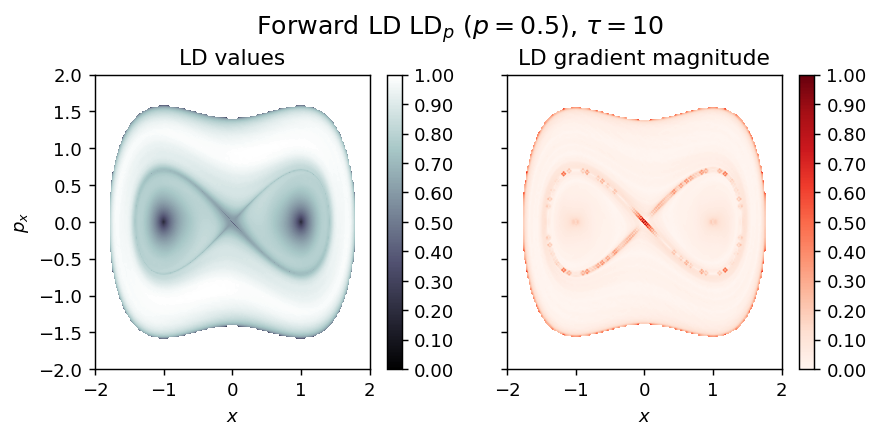
../_images/examples_88_0.png 
LD_backward = compute_lagrangian_descriptor(grid_parameters, vector_field, -tau, p_value)
draw_lagrangian_descriptor(LD_backward, 'backward', grid_parameters, tau, p_value)
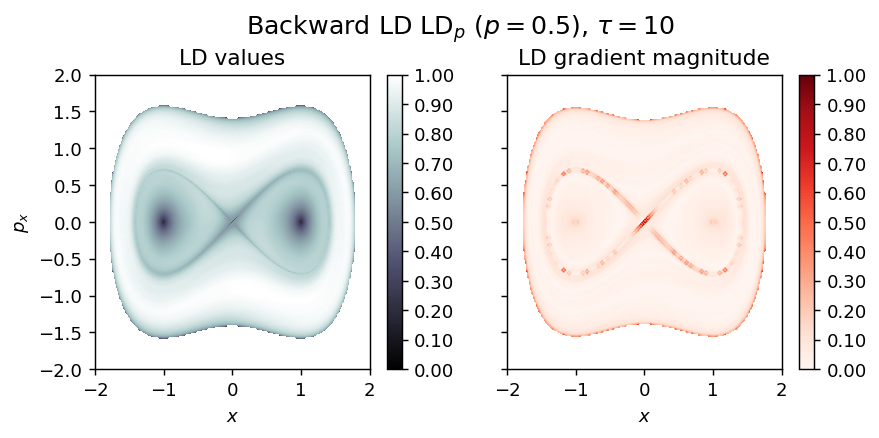
../_images/examples_89_0.png 
LD_total = LD_forward + LD_backward
draw_lagrangian_descriptor(LD_total, 'total', grid_parameters, tau, p_value)
../_images/examples_90_0.png
The Method of Lagrangian Descriptors